12. 性能优化

12.1. 总体优化策略 (Overall Performance Optimization Strategies)

在GCU上的性能优化主要包含以下四个方面：

  1. 利用并行计算的特性将计算平均的展开到多个线程上进行

  2. 利用多级内存并优化数据搬运方式，最大化内存吞吐量和带宽利用率

  3. 优化核心循环的指令排布，最大化指令吞吐量和算力利用率

  4. 优化设备内存的分配策略，以降低内存颠簸的影响

在下面的GCU计算数据流图，每次计算都是从设备内存开始输入数据，并将输入回写设备内存。在GCU210上并没有末级缓存，只有GCU300及更高的架构包含末级缓存。末级缓存对开发人员来说几乎是透明的。橙色箭头表示相邻两级之间的数据传输方式，在GCU210和GCU300上都支持。草绿色箭头表示末级缓存和私有存储之间的直接数据传输方式，蓝色箭头表示末级缓存和寄存器之间的直接数据传输方式，在GCU300及更高的架构上支持。

对于开发人员来说，需要将计算均匀的分配给多个线程，且线程数最好等于设备上SIP的数量。通过数据搬运方式和指令排布等方面的优化，获得高的算力利用率和带宽利用率。

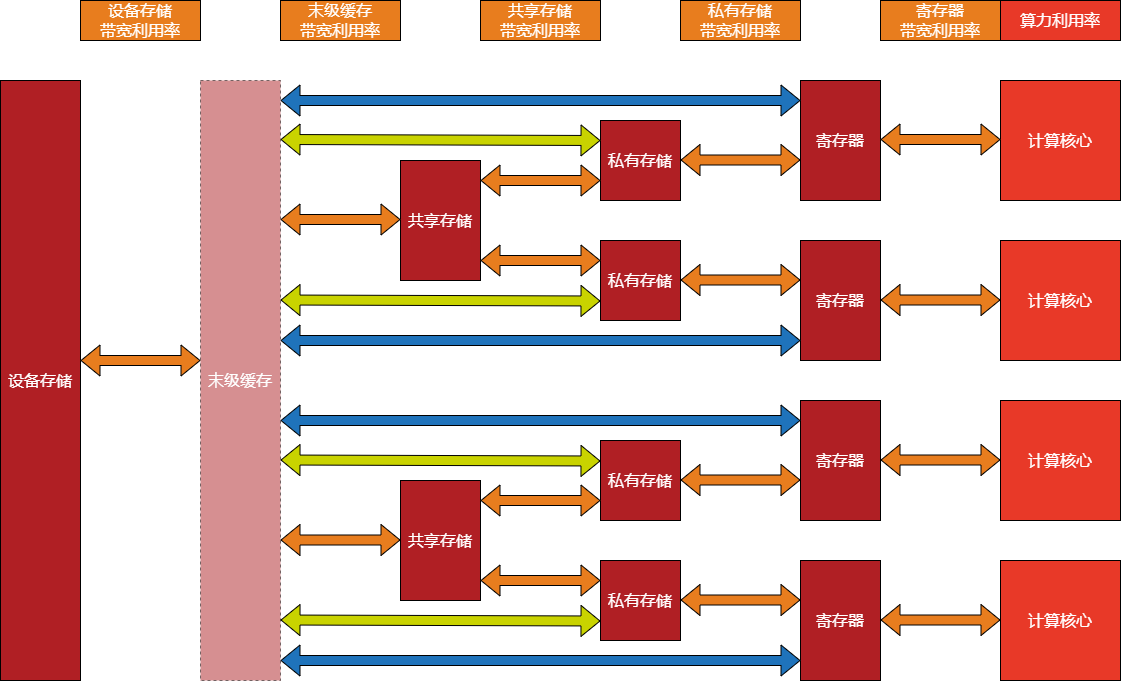
GCU计算数据流图

图 12.1.1 GCU计算数据流图

12.2. 利用率分析 (Utilization Analysis)

利用topsprofiler或者其它性能观察的工具，可获得算子的运行时间。结合算子的计算量和数据量，可以分析算力利用率和带宽利用率。本节的分析使用下表中的术语。

术语

定义

算力(math rate)

硬件进行计算的吞吐能力，单位为float point operations per second, 缩写为Flops

设备标称算力(device math rate)

GCU/GPU等设备spec上标称的算力，单位为Flops

实测算力(measured math rate)

在运行计算过程中实测达到的算力，单位为Flops

设备标称带宽(device bandwidth)

GCU/GPU等设备spec上标称的带宽，单位为Byte/s

实测带宽(measured bandwidth)

在运行计算过程中实测达到的带宽，单位为Byte/s

计算量(number of operations)

计算的数量，单位为Ops

数据量(number of bytes)

搬运的数据量，单位为Bytes

算术密度(arithmetic intensity)

某个计算的计算量和数据量的比值

设备算力带宽比(device ratio of math rate versus bandwidth)

设备的标称算力和标称带宽的比值

运行时间(duration)

计算的运行时间，单位为Seconds

访存时间(memory time)

访问memory搬运数据的时间，包括读数据和写数据的时间

计算时间(math time)

在矩阵/向量/特殊等运算器上完成计算的时间

每元素字节数(byte per element)

指数据类型的每元素字节数，缩写为BPE

每元素计算量(operation per element)

指每个元素上的计算量，缩写为OPE

number of Clusters

计算单元集群的数量

number of SIPs

每个计算单元集群中SIP的数量

number of MACs

SIP中矩阵运算器的吞吐。和数据类型有关，不同数据类型可能不同

number of Elementwises

SIP中向量运算器的吞吐。和数据类型有关，不同数据类型可能不同。对应下表中16-bit / 32-bit float/integer运算的throughput

number of SFUs

SIP中特殊运算器的吞吐。仅支持FP32数据类型，对应下表中特殊运算的throughput: 32-bit floating-point reciprocal, reciprocal square root, base-2 logarithm等

SIP frequency

SIP的运行频率，单位为Hz

算力利用率分析

2D/1D/SFU算力利用率可计算为测得算力和设备标称算力的比值，其中测得算力可计算为计算量和运行时间的比值：

(12.2.1)\[\frac{measured\ math\ rate}{device\ math\ rate}=\frac{number\ of\ operations/ duration}{device\ math\ rate}=\frac{number\ of\ operations}{device\ math\ rate * duration}\]

硬件设备的算力

如2.1节所述，GCU的SIP中有不同的运算器，其中矩阵运算器、向量运算器和特殊运算器，分别负责2D算子（如Dot, Conv）、1D算子(如elementwise op)和特殊函数（如超越函数）的计算。

GCU的硬件算力规格可计算如下：

  • 2D算力：\(number\ of\ Clusters \times number\ of\ SIPs \times number\ of\ MACs \times SIP\ frequency \times 2\)。注意不同数据类型的\(number\ of\ MACs\)一般不同。乘2是因为矩阵运算器的\(MAC\)包含乘加两个操作。

  • 1D算力：\(number\ of\ Clusters \times number\ of\ SIPs \times number\ of\ Elementwises \times SIP\ frequency\)。注意不同数据类型的 \(number\ of\ Elementwises\)一般不同。如果某个数据类型下的向量运算器支持乘加，则1D算力再乘2为：\(number\ of\ Clusters \times number\ of\ SIPs \times number\ of\ Elementwises \times SIP\ frequency \times 2\)。

  • 特殊函数算力：\(number\ of\ Clusters \times number\ of\ SIPs \times number\ of\ SFUs \times SIP\ frequency\)

Dot算子的计算量(number of operations)

典型的Dot算子完成\(C=A \times B\) 的矩阵-矩阵乘法，其中 左操作数矩阵\(A\) 为 \(M\)行 \(K\) 列，右操作数矩阵\(B\) 为\(K\) 行 \(N\) 列，结果矩阵\(C\) 为\(M\) 行 \(N\) 列。计算可表示为：

(12.2.2)\[[M \times N] = Dot ([M \times K], [K \times N])\]

矩阵\(C\) 共有\(M \times N\) 个元素，每个元素的值来自于 \(K\)对元素的点乘(dot product)之和。故计算量之和为 \(M \times N \times K\)个乘加(fused multiply-add, FMA)，每个乘加包括乘法和加法两个操作。因此Dot算子计算量为：

(12.2.3)\[2 \times M \times N \times K\]

Conv算子的计算量(number of operations)

典型的Convolution forward完成Output=Conv(Input feature, Weight)的卷积运算。对于2d convolution，Input feature, Weight, Output均为4维。Input feature维度为\([N, H_i, W_i, C_i]\)，其中\(N\)为batch数量，\(H_i\)和\(W_i\)分别为Input feature的高和宽, \(C_i\)为输入channel的数量。Weight的维度为\([R, S, C_i, C_o]\)，其中\(R\) 和 \(S\) 分别为filter的高和宽，\(C_i\) 为输入channel的数量，\(C_o\) 为输出channel的数量。Output的维度为 \([N, H_o, W_o, C_o]\), 其中\(N\)为batch数量，\(H_o\)和\(W_o\)分别为Output的高和宽, \(C_o\)为输出channel的数量。可表示为：

(12.2.4)\[[N, H_o, W_o, C_o] = Conv ( [N, H_i, W_i, C_i], [R, S, C_i, C_o] )\]

Convolution forward共进行\(N \times H_o \times W_o \times C_i \times C_o \times R \times S\) 个乘加，每个乘加包括乘法和加法两个操作。因此Convolution farward算子计算量为：

(12.2.5)\[2 \times N \times H_o \times W_o \times C_i \times C_o \times R \times S\]

4. 1D算子的计算量(number of operations)

1D算子包含种类繁多的算子类型。以Elementwise 类型的算子为例，计算发生在每一个元素上，因此计算量和元素个数\(N\)成正比，Elementwise 算子计算量可表示为：

(12.2.6)\[N \times OPE\]

对于Elementwise的二元算子（binary op） Add, Sub, Mul, Div，OPE = 1，因此计算量为\(N\)。

带宽利用率分析

算子的带宽利用率可计算为测得带宽和设备标称带宽的比值：

(12.2.7)\[\frac{measured\ bandwidth}{device\ bandwidth} = \frac{number\ of\ bytes/duration}{device\ bandwidth} = \frac{number\ of\ bytes}{device\ bandwidth*duration}\]

硬件设备的带宽

硬件设备通常具备多级memory，从最外层（远离计算单元）到最内层（靠近计算单元），带宽逐渐增加。因此，更容易被卡在最外层memory的带宽上。如3.3节中所述，GCU最外层的memory为设备内存，一般为DDR或HBM。具体的带宽数据请参考硬件Spec。本节主要关注设备内存的带宽利用率。

Dot算子的数据量(number of bytes)

Dot算子有两个输入tensor和一个输出tensor，分别读和写设备内存，消耗内存带宽。Dot算子的数据量为：

(12.2.8)\[(M \times K + K \times N + M \times N)\times BPE (Bytes)\]

如果在GCU的多个SIP之间，没有完全共享Dot的右操作数，则右操作数被多个SIP重复搬运，导致数据量变大。计算数据量时右操作数需乘以被搬运的次数。

Conv算子的数据量(number of bytes)

Convolution forward 有两个输入tensor和一个输出tensor，分别读和写设备内存。Convolution forward算子的数据量为：

(12.2.9)\[(N \times H_i \times W_i \times C_i + R \times S \times C_i \times C_o + N \times H_o \times W_o \times C_o ) \times BPE (Bytes)\]

如果在GCU的多个sip之间，没有完全共享Weight，则Weight被多个SIP重复搬运，导致数据量变大。计算数据量时Weight需乘以被搬运的次数。

1D算子的数据量(number of bytes)

1D算子的数据量也是其读和写设备内存的数据量之和。以Elementwise的二元算子（binary op） Add, Sub, Mul, Div为例，设共计N个元素，则其数据量为：

(12.2.10)\[(\text{lhs size + rhs size + output size}) = (N + N + N) \times BPE = 3N \times BPE (Bytes)\]

算术密度和瓶颈分析

在GCU上，可能有两种性能瓶颈：带宽、计算。我们考虑一个简化的计算模型：读取输入数据、计算、写回结果数据。在GCU上，读写设备内存和计算可以并行。将读取输入数据和写回结果数据的时间之和记为 \(memory\ time\) ，计算时间记为\(math\ time\) ，则算子的运行时间\(duration = max(memory\ time, math\ time)\)。当\(memory\ time\)更长时为带宽瓶颈，当\(math\ time\)更长时则为计算瓶颈。

\(memory\ time\)可被计算如下：

(12.2.11)\[\frac{number\ of\ bytes}{device\ bandwidth}\]

\(math\ time\)可被计算如下：

(12.2.12)\[\frac{number\ of\ operations}{device\ math\ rate}\]

当为计算瓶颈时，即\(math time > memory time\)，可得:

(12.2.13)\[\frac{number\ of\ operations}{device\ math\ rate} > \frac{number\ of\ bytes}{device\ bandwidth} \Longrightarrow \frac{number\ of\ operations}{number\ of\ bytes} > \frac{device\ math\ rate}{device\ bandwidth}\]

\(\frac{number\ of\ operations}{number\ of\ bytes}\) 和具体算子/算法有关，称为算术密度(arithmetic intensity)。\(\frac{device\ math\ rate}{device\ bandwidth}\) 则和具体硬件设备相关，对特定的GCU是特定的值，称作设备算力带宽比。算术密度和设备算力带宽比的单位均为Flops/Byte。当算术密度 > 设备算力带宽比时为计算瓶颈，反之为带宽瓶颈。

Dot算子的算术密度(arithmetic intensity)

(12.2.14)\[\frac{ 2 \times M \times N \times K}{ (M \times K + K \times N + M \times N) \times BPE}\]

Conv算子的算术密度(arithmetic intensity)

(12.2.15)\[\frac{ 2 \times N \times H_o \times W_o \times C_i \times C_o \times R \times S}{(N \times H_i \times W_i \times C_i + R \times S \times C_i \times C_o + N \times H_o \times W_o \times C_o ) \times BPE}\]

1D算子的算术密度(arithmetic intensity)

以Elementwise binary op 为例，其算术密度为：

(12.2.16)\[\frac{N}{3N\times BPE} = \frac{1}{3 \times BPE}\]

12.3. 编译优化（Compilation Optimization）

指定循环的属性

循环展开

默认情况下（不加编译指示），编译器会根据自身判断，是否展开循环或展开多少次循环。然而，#pragma unroll指令可用于控制任何给定循环的展开，它必须放置在循环语句之前，并且仅适用于该循环。它后面可以跟随一个常量表达式。如果常量表达式不存在，并且循环次数是常量，循环将被完全展开。如果常量表达式的计算结果为 1，编译器将不会展开循环。如果常量表达式的结果为非正整数或大于int数据类型可表示的最大值的整数，则编译指示将被忽略。

struct S1_t { static const int value = 4; };
template <int X, typename T2>
__device__ void foo(int *p1, int *p2) {

// 没有指定展开次数，编译器会根据自身条件判断展开次数，
// 对于常量小循环，通常会完全展开
#pragma unroll
for (int i = 0; i < 12; ++i)
  p1[i] += p2[i]*2;

// 告知编译器强制展开8次
#pragma unroll (X+1)
for (int i = 0; i < 12; ++i)
  p1[i] += p2[i]*4;

// unroll value = 1, 禁止循环展开，等价于 #pragma nounroll
#pragma unroll 1
for (int i = 0; i < 12; ++i)
  p1[i] += p2[i]*8;

// 告知编译器强制展开4次
#pragma unroll (T2::value)
for (int i = 0; i < 12; ++i)
  p1[i] += p2[i]*16;
}

__global__ void bar(int *p1, int *p2) {
  foo<7, S1_t>(p1, p2);
}