11. 性能优化¶
本章节假设用户已经了解GCU硬件信息,及GCU编程指南相关内容,并对Triton有基本的了解。在此基础上,给出TritonGCU上一些典型的性能优化场景建议,以帮助用户写出更好性能的TritonGCU kernel(以下简称kernel)。
11.1. grid && num_warps¶
配置适当的GridDim和BlockDim(num_warps),将并行度以循环方式放入kernel内。
在当前GCU300硬件平台上,因为kernel启动开销无法被完全掩盖,使得Triton kernel以大于GCU硬件资源数量的GridDim和BlockDim并行执行时,会引入额外的调度开销,从而增加算子执行时间,降低性能,这一性能损失在kernel计算量较小时尤为明显。因此,建议将kernel间的并行度,尽可能以循环方式放入kernel内,从而避免额外的调度开销。建议的配置方式是,尽量以一次刚好占满所有计算资源所需的GridDim和BlockDim(num_warps)来配置,从而避免额外的调度开销。在kernel准备就绪后,使用Triton-Autotuner重新筛选最佳BLOCK_SIZE。
GCU300:硬件有2个DIE,每个DIE有12个SIP,总计24个SIP。TRITONGCU将Thread(warp)映射到SIP,同时,因为同一个Block内的所有Threads(warps)不能跨DIE启动的硬件限制,为了获得计算资源的最大利用率,推荐的GridDim和BlockDim(num_warps)配置方式为
GridDim(x,y,z) |
BlockDim(x,y,z) |
num_warps |
说明 |
|---|---|---|---|
(6,1,1) |
(4,1,1) |
4 |
每个硬件DIE上,并行3个Blocks,每个Block有4个Threads |
(12,1,1) |
(2,1,1) |
2 |
|
(24,1,1) |
(1,1,1) |
1 |
|
(2,1,1) |
(8,1,1) |
8 |
有三分之一的硬件算力资源空闲,非带宽瓶颈算子不推荐尝试 |
注意 在当前TritonGCU版本上(Triton官方默认参数),num_warps被默认设置为4
GCU400:硬件有4个DIE,每个DIE有6个SIP,每个SIP又包含了8个sub-thread,总计24个SIP,192个sub-thread。不同于GCU300上的映射关系,在GCU400上,TritonGCU将Thread(warp)映射到硬件的sub-thread,为了获得计算资源的最大利用率,推荐的GridDim和BlockDim(num_warps)配置方式为
GridDim(x,y,z) |
BlockDim(x,y,z) |
num_warps |
说明 |
|---|---|---|---|
(24,1,1) |
(8,1,1) |
8 |
|
(48,1,1) |
(4,1,1) |
4 |
【示例 1】
以官方tutorials中vector-add为例:
import triton_gcu.triton
import triton
import torch
import triton.language as tl
import torch_gcu
@triton.jit
def add_kernel(x_ptr,
y_ptr,
output_ptr,
n_elements,
BLOCK_SIZE: tl.constexpr,
):
pid = tl.program_id(axis=0)
block_start = pid * BLOCK_SIZE
offsets = block_start + tl.arange(0, BLOCK_SIZE)
mask = offsets < n_elements
x = tl.load(x_ptr + offsets, mask=mask)
y = tl.load(y_ptr + offsets, mask=mask)
output = x + y
tl.store(output_ptr + offsets, output, mask=mask)
def add(x: torch.Tensor, y: torch.Tensor):
output = torch.empty_like(x)
n_elements = output.numel()
grid = lambda meta: (triton.cdiv(n_elements, meta['BLOCK_SIZE']), )
add_kernel[grid](x, y, output, n_elements, BLOCK_SIZE=128)
return output
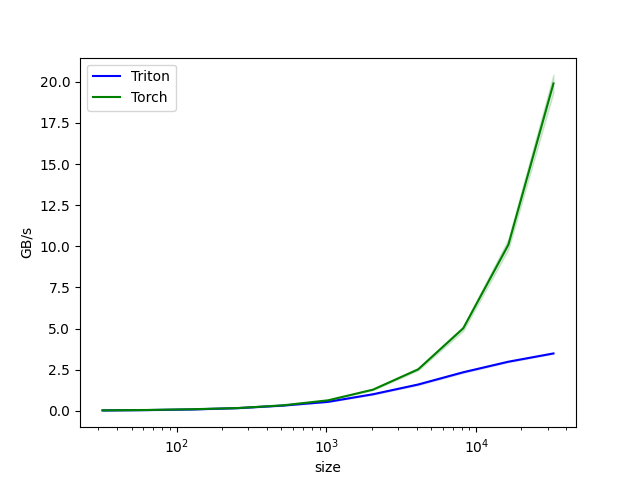
【示例 2】
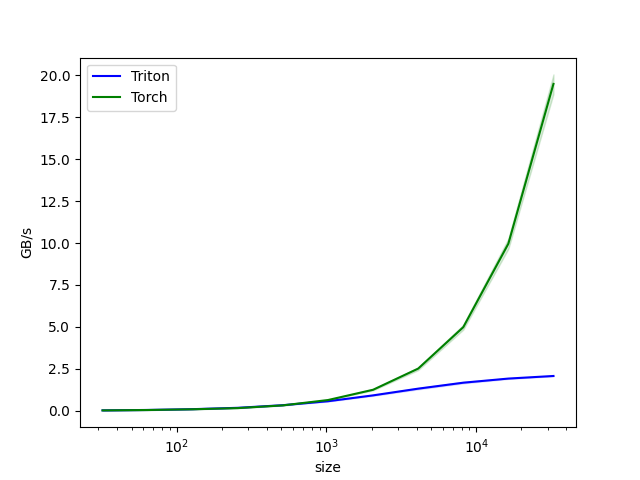
对kernel进行增加一层循环搬运的改写,方式如下:
def add_kernel(x_ptr,
y_ptr,
output_ptr,
n_elements,
SIZE_PER_THREAD,
BLOCK_SIZE: tl.constexpr,
GRID_NUM: tl.constexpr,
):
pid = tl.program_id(axis=0)
for i in range(0, SIZE_PER_THREAD, BLOCK_SIZE):
block_start = pid * SIZE_PER_THREAD + i
offsets = block_start + tl.arange(0, BLOCK_SIZE)
mask = offsets < n_elements
x = tl.load(x_ptr + offsets, mask=mask)
y = tl.load(y_ptr + offsets, mask=mask)
output = x + y
tl.store(output_ptr + offsets, output, mask=mask)
def add(x: torch.Tensor, y: torch.Tensor):
output = torch.empty_like(x)
n_elements = output.numel()
grid = (6,1,1)
SIZE_PER_THREAD = (n_elements + 5) // 6
add_kernel[grid](x, y, output, n_elements,
SIZE_PER_THREAD, BLOCK_SIZE=128, GRID_NUM=6)
return output
11.2. BLOCK_SIZE¶
在GCU300硬件上, DTE存在一定的启动开销,因此在不超过memory使用限制的前提下, 一次搬运越多的数据,性能越好。在kernel实现时, 一般load/store buffer size和BLOCK_SIZE相关,所以一定程度上可以认为选择一个合适的BLOCK_SIZE,可以带来更好的性能(相比GPU-kernel,GCU的Triton-kernel BLOCK_SIZE倾向于更大一些)
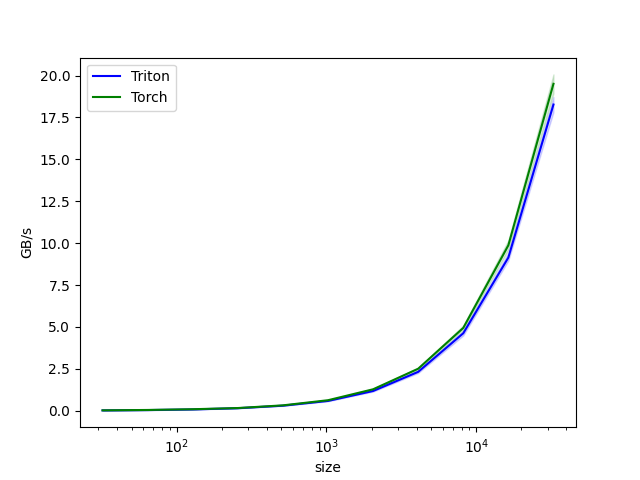
对于【示例 1】的场景在增加了kernel内循环的基础上,进一步选择BLOCK_SIZE=1024,可以得到如下性能对比: 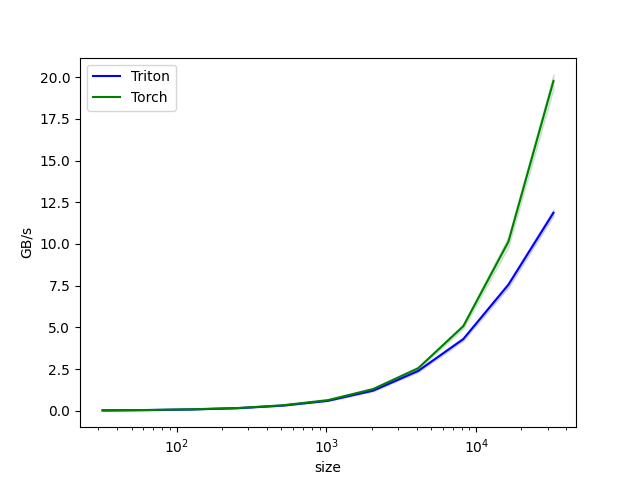
11.3. 以连续方式加载数据,避免低效的随机地址访问¶
在当前GCU硬件平台上,离散地址的数据访问是非常低效的。TritonGCU会尽可能的在编译期分析出地址连续的load/store场景,从而转成DTE访问。 但是这种分析,依然存在不少的限制:
load的地址偏移向量是完全动态的,如参数传入(如示例 3)
load的地址偏移向量的计算存在求模运算,这可能会造成某些mask掉的数据是对某一块数据的多次读取,另外存在的余数场景,也会使分析和代码生成的复杂度会极大的提高(如示例 4)
针对多维情况下需要mask掉的数据也采用各个维度分别mask的方案,不要展开成1维进行处理(如示例 5)
make_tensor_ptr接口的参数: strides, 是来源于kernel的形参时,该场景无法在编译期被分析(如示例 6)
因此,建议用户尽量在kernel内显式的描述连续load/store,以避免低效的随机地址访问。
【示例 3】
这个示例中有2个load操作,分别是tensor:x和tensor:o,它们采用了不同的内存访问方式: 其中x需要load的地址偏移向量是动态的,需要从内存load得到,该地址偏移量无法分析其连续性, 因此这个load内存访问是采用离散式的内存访问方式。 然而针对o的load的地址偏移向量就是静态的,这个load内存访问会被优化成连续的地址访问方式。 以官方test_core中test_load_store_reverse_offset为例:
def test_load_store_reverse_offset(dtype, N, device):
@triton.jit
def load_store_kernel(X, O, Z, N: tl.constexpr):
offsets = tl.program_id(axis=0) * N + tl.arange(0, N)
mask = offsets < N
o = tl.load(O + offsets, mask=mask)
x = tl.load(X + o, mask=mask)
tl.store(Z + o, x, mask=mask)
x = numpy_random(N, dtype_str=dtype)
o = np.array(range(N)[::-1], dtype=np.int32)
x_tri = to_triton(x, device=device)
o_tri = to_triton(o, device=device)
z_tri = to_triton(np.empty(N, dtype=dtype), device=device, dst_type=dtype)
load_store_kernel[(1,)](x_tri, o_tri, z_tri, N, num_warps=1)
assert torch.equal(z_tri, x_tri)
【示例 4】
这个示例存在对地址偏移向量求%的计算,以官方tutorials中triton-matmul为例:
import triton
import torch
import triton.language as tl
import triton_gcu.triton
import torch_gcu
@triton.jit
def matmul_kernel(
a_ptr, b_ptr, c_ptr, M, N, K,
stride_am, stride_ak, stride_bk, stride_bn, stride_cm, stride_cn,
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr,
BLOCK_SIZE_K: tl.constexpr, GROUP_SIZE_M: tl.constexpr,
ACTIVATION: tl.constexpr,
):
"""Kernel for computing the matmul C = A x B.
A has shape (M, K), B has shape (K, N) and C has shape (M, N)
"""
pid = tl.program_id(axis=0)
num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
num_pid_in_group = GROUP_SIZE_M * num_pid_n
group_id = pid // num_pid_in_group
first_pid_m = group_id * GROUP_SIZE_M
group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
pid_m = first_pid_m + (pid % group_size_m)
pid_n = (pid % num_pid_in_group) // group_size_m
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
offs_k = tl.arange(0, BLOCK_SIZE_K)
a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
accumulator = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
for k in range(0, tl.cdiv(K, BLOCK_SIZE_K)):
a = tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K,
other=0.0)
b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K,
other=0.0)
accumulator += tl.dot(a, b)
a_ptrs += BLOCK_SIZE_K * stride_ak
b_ptrs += BLOCK_SIZE_K * stride_bk
if ACTIVATION == "leaky_relu":
accumulator = leaky_relu(accumulator)
c = accumulator.to(tl.float32)
offs_cm = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
offs_cn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
c_ptrs = c_ptr + stride_cm * offs_cm[:, None] + stride_cn * offs_cn[None, :]
c_mask = (offs_cm[:, None] < M) & (offs_cn[None, :] < N)
tl.store(c_ptrs, c, mask=c_mask)
@triton.jit
def leaky_relu(x):
x = x + 1
return tl.where(x >= 0, x, 0.01 * x)
def matmul(a, b, activation=""):
assert a.shape[1] == b.shape[0], "Incompatible dimensions"
assert a.is_contiguous(), "Matrix A must be contiguous"
assert b.is_contiguous(), "Matrix B must be contiguous"
M, K = a.shape
K, N = b.shape
c = torch.empty((M, N), device=a.device, dtype=a.dtype)
grid = lambda META: (
triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(N, META['BLOCK_SIZE_N']),
)
matmul_kernel[grid](
a, b, c,
M, N, K,
a.stride(0), a.stride(1),
b.stride(0), b.stride(1),
c.stride(0), c.stride(1),
BLOCK_SIZE_M = 16,
BLOCK_SIZE_N = 16,
BLOCK_SIZE_K = 16,
GROUP_SIZE_M = 8,
ACTIVATION=activation,
num_warps=4
)
return c
torch.manual_seed(0)
a = torch.randn((128, 64), dtype=torch.float32).gcu()
b = torch.randn((64, 128), dtype=torch.float32).gcu()
triton_output = matmul(a, b)
torch_output = torch.matmul(a, b)
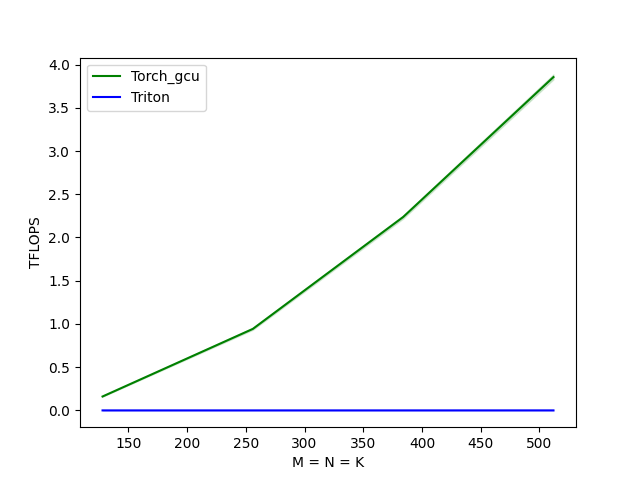
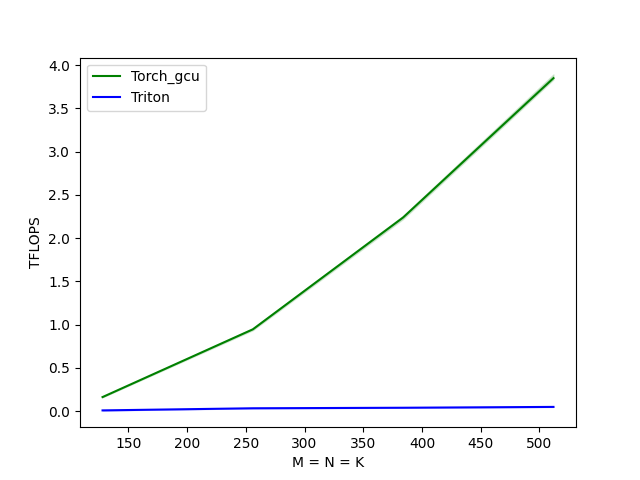
此时发现性能并没有太大变化,这里就是因为load的地址偏移向量的计算存在了求模运算,load/store使用了离散地址进行了数据访问。 尝试以下优化方案(为了重点关注修改内容,下述只显示修改代码)
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
源示例中上述2行修改为:
offs_am = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
offs_bn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
a = tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
同时还需要修改源示例load函数中对应的mask参数:
mask = (offs_am < M)[:,None] & (offs_k[None, :] < K - k * BLOCK_SIZE_K)
a = tl.load(a_ptrs, mask, other=0.0)
mask = (offs_k[:, None] < K - k * BLOCK_SIZE_K) & (offs_bn < N)[None,:]
b = tl.load(b_ptrs, mask, other=0.0)
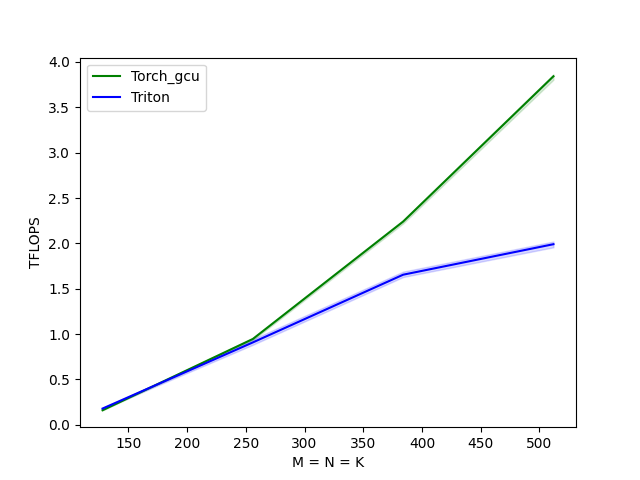
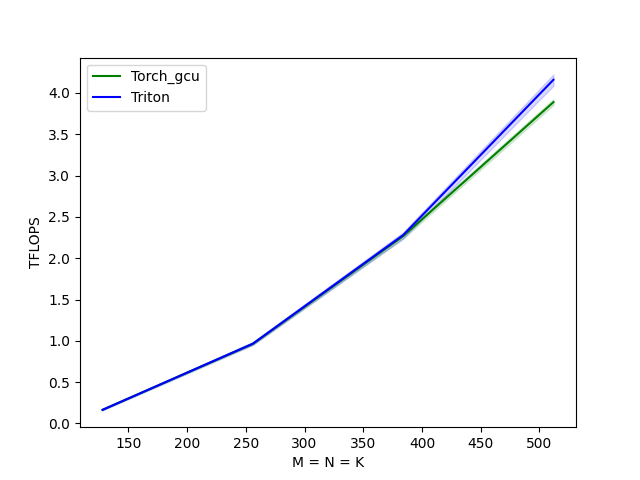
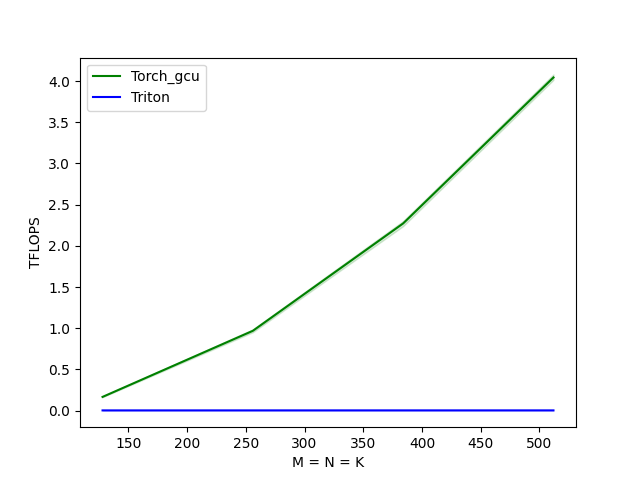
【示例 5】
这个示例不符合多维tensor的每个维度都需要一个mask信息的约束,否则要求shape可以整除block_size。由于我们无法进行这个约束限制,因此使用该方式的load都会变成离散数据处理。以官方test_core中test_masked_load_shared_memory为例:
def test_masked_load_shared_memory(dtype, device):
check_type_supported(dtype, device)
M = 32
N = 32
K = 16
in1 = torch.rand((M, K), dtype=dtype, device=device)
in2 = torch.rand((K, N), dtype=dtype, device=device)
out = torch.zeros((M, N), dtype=dtype, device=device)
@triton.jit
def _kernel(in1_ptr, in2_ptr, output_ptr, in_stride, in2_stride,
out_stride, in_numel, in2_numel, out_numel,
M: tl.constexpr, N: tl.constexpr, K: tl.constexpr):
M_offsets = tl.arange(0, M)
N_offsets = tl.arange(0, N)
K_offsets = tl.arange(0, K)
in_offsets = M_offsets[:, None] * in_stride + K_offsets[None, :]
in2_offsets = K_offsets[:, None] * in2_stride + N_offsets[None, :]
x = tl.load(in1_ptr + in_offsets, mask=in_offsets < M * K)
w = tl.load(in2_ptr + in2_offsets, mask=in2_offsets < K * N)
o = tl.dot(x, w, out_dtype=tl.float32)
output_offsets = M_offsets[:, None] * out_stride + N_offsets[None, :]
tl.store(output_ptr + output_offsets, o, mask=output_offsets < M * N)
pgm = _kernel[(1, )](in1, in2, out, in1.stride()[0], in2.stride()[0],
out.stride()[0], in1.numel(), in2.numel(),
out.numel(), M=M, N=N, K=K)
reference_out = torch.matmul(in1, in2)
torch.testing.assert_close(out, reference_out, atol=1e-2, rtol=0)
优化方案和上个示例比较类似,我们只关注针对mask的处理,benchmark数值不再展示:
x = tl.load(in1_ptr + in_offsets, mask=in_offsets < M * K)
w = tl.load(in2_ptr + in2_offsets, mask=in2_offsets < K * N)
tl.store(output_ptr + output_offsets, o, mask=output_offsets < M * N)
该示例我们只需要修改源示例load|store函数中对应的mask参数,就可以变成连续的数据处理:
mask_x = (M_offsets < M)[:, None] & (K_offsets < K)[None, :]
x = tl.load(in1_ptr + in_offsets, mask_x)
mask_w = (K_offsets < K)[:, None] & (N_offsets < N)[None, :]
w = tl.load(in2_ptr + in2_offsets, mask_w)
mask_st = ((M_offsets < M)[:, None] & (N_offsets < N)[None, :])
tl.store(output_ptr + output_offsets, o, mask_st)
【示例 6】
该示例的stride参数就是kernel的形参,它无法在编译期进行分析的,只能用离散的数据访问方式。 后续预期会在运行期来进行分析,但同时也会带来性能损失
@triton.jit
def load_kernel_block(
a_ptr, b_ptr,
M, N, K,
stride_am, stride_an, stride_ak,
block_shape_m, block_shape_n, block_shape_k,
stride_bm, stride_bn, stride_bk,
BLOCK_M: tl.constexpr, BLOCK_N: tl.constexpr, BLOCK_K: tl.constexpr
):
a_block_ptr = tl.make_block_ptr(
base=a_ptr, shape=(M, N, K), strides=(stride_am, stride_an, stride_ak),
offsets=(0, 0, 0), block_shape=(BLOCK_M, BLOCK_N, BLOCK_K),
order=(2, 1, 0))
b_block_ptr = tl.make_block_ptr(
base=b_ptr, shape=(block_shape_m, block_shape_n, block_shape_k),
strides=(stride_bm, stride_bn, stride_bk), offsets=(0, 0, 0),
block_shape=(BLOCK_M, BLOCK_N, BLOCK_K), order=(2, 1, 0))
a = tl.load(a_block_ptr, boundary_check=(0, 1, 2), padding_option="zero")
tl.store(b_block_ptr, a, boundary_check=(0, 1, 2))
针对该问题优化方案有2种: 1. 编译期不知道stride的值:
def load_kernel_block(
a_ptr, b_ptr,
M, N, K,
stride_am, stride_an, stride_ak,
block_shape_m, block_shape_n, block_shape_k,
stride_bm, stride_bn, stride_bk,
BLOCK_M: tl.constexpr, BLOCK_N: tl.constexpr, BLOCK_K: tl.constexpr
):
从参数传递的角度来看,可以把上文函数定义部分的stride参数标记为tl.constexpr,当然这也会带来一些负作用,造成stride每次发生变化时都会重新编译,而不是命中cache:
def load_kernel_block(
a_ptr, b_ptr,
M, N, K,
stride_am: tl.constexpr, stride_an: tl.constexpr, stride_ak: tl.constexpr,
block_shape_m, block_shape_n, block_shape_k,
stride_bm: tl.constexpr, stride_bn: tl.constexpr, stride_bk: tl.constexpr,
BLOCK_M: tl.constexpr, BLOCK_N: tl.constexpr, BLOCK_K: tl.constexpr
):
编译期已经知道stride的值:
a_block_ptr = tl.make_block_ptr(
base=a_ptr, shape=(M, N, K), strides=(stride_am, stride_an, stride_ak),
offsets=(0, 0, 0), block_shape=(BLOCK_M, BLOCK_N, BLOCK_K),
order=(2, 1, 0))
b_block_ptr = tl.make_block_ptr(
base=b_ptr, shape=(block_shape_m, block_shape_n, block_shape_k),
strides=(stride_bm, stride_bn, stride_bk), offsets=(0, 0, 0),
block_shape=(BLOCK_M, BLOCK_N, BLOCK_K), order=(2, 1, 0))
直接把相关stride的参数替换成具体的数值,例如stride_m=32,stride_n=4,stride_k=1:
a_block_ptr = tl.make_block_ptr(
base=a_ptr, shape=(M, N, K), strides=(32, 4, 1),
offsets=(0, 0, 0), block_shape=(BLOCK_M, BLOCK_N, BLOCK_K),
order=(2, 1, 0))
b_block_ptr = tl.make_block_ptr(
base=b_ptr, shape=(block_shape_m, block_shape_n, block_shape_k),
strides=(32, 4, 1), offsets=(0, 0, 0),
block_shape=(BLOCK_M, BLOCK_N, BLOCK_K), order=(2, 1, 0))
11.4. pingpong 的使能¶
1D计算pingpong¶
【示例 7】 本实例是一种针对大数据量(大于256k)的性能友好的写法,设置所有并行计算任务的数量等于硬件基础计算单元数量的方式,保证每个硬件基础计算单元只会启动一次,减小调度开销。
在num_stages的数量计算中,核心计算占用一个stage,比如num_stages=3,占用2份DTE和share memory相关资源,若num_stages小于3则表示关闭pingpong
说明:为了保持和Triton GPU生态行为一致性,非2D计算的pingpong,需要对kernel内的逐个for循环设置 num_stages。
GRID_DIM_X = 6
@triton.jit
def add_kernel_1D_loop(x_ptr, # *Pointer* to first input vector.
y_ptr, # *Pointer* to second input vector.
output_ptr, # *Pointer* to output vector.
n_elements, # Size of the vector.
BLOCK_SIZE: tl.constexpr,
GRID_DIM_X: tl.constexpr,
num_stages: tl.constexpr
):
# There are multiple 'programs' processing different data. We identify which program
# we are here:
pid = tl.program_id(axis=0) # We use a 1D launch grid so axis is 0.
num_tile = (n_elements + BLOCK_SIZE - 1) // BLOCK_SIZE
for tile_id in tl.range(pid, num_tile, GRID_DIM_X, num_stages=num_stages):
# tl.device_print("tile_id", tile_id)
block_start = tile_id * BLOCK_SIZE
offsets = block_start + tl.arange(0, BLOCK_SIZE)
# Create a mask to guard memory operations against out-of-bounds accesses.
mask = offsets < n_elements
x = tl.load(x_ptr + offsets, mask=mask)
y = tl.load(y_ptr + offsets, mask=mask)
output = x + y
# Write x + y back to DRAM.
tl.store(output_ptr + offsets, output, mask=mask
def add(x: torch.Tensor, y: torch.Tensor):
# We need to preallocate the output.
output = torch.empty_like(x)
n_elements = output.numel()
block_size = 8192
#launch block number should be less than or equal to proposed GRID_DIM_X
grid = lambda meta: (min(GRID_DIM_X, (triton.cdiv(n_elements, meta['BLOCK_SIZE']))), )
add_kernel_1D_loop[grid](x, y, output, n_elements, BLOCK_SIZE=block_size,
GRID_DIM_X=GRID_DIM_X, num_warps=4, num_stages=3)
return output
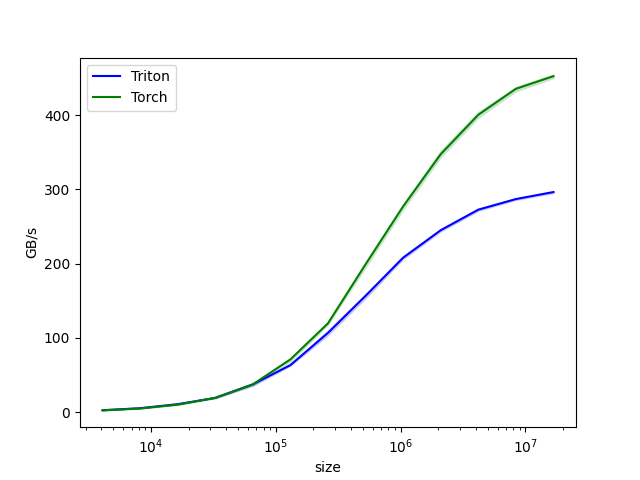
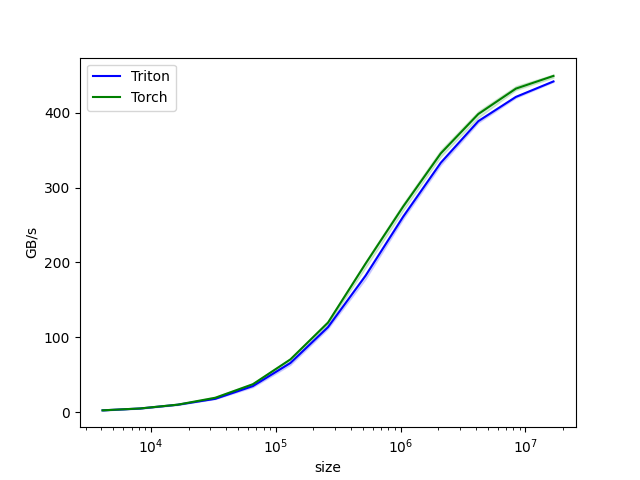
结论:pingpong 开启后,输入数据在100K以上数据性能可以保持稳定不下降,中和了block_size对性能的影响。
2D计算pingpong¶
2D计算推荐默认开启pingpong,默认的num_stages=3,用户也可以根据各个算子的需求自己设置,示例如下写在launch参数上,若num_stages小于3则表示关闭pingpong。
【示例 8】
本示例是【示例 4】的launch部分配置pingpong部分的说明:
def matmul(a, b, activation=""):
# Check constraints.
assert a.shape[1] == b.shape[0], "Incompatible dimensions"
assert a.is_contiguous(), "Matrix A must be contiguous"
assert b.is_contiguous(), "Matrix B must be contiguous"
M, K = a.shape
K, N = b.shape
# Allocates output.
c = torch.empty((M, N), device=a.device, dtype=a.dtype)
# 1D launch kernel where each block gets its own program.
grid = lambda META: (
triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(N, META['BLOCK_SIZE_N']),
)
matmul_kernel[grid](
a, b, c,
M, N, K,
a.stride(0), a.stride(1),
b.stride(0), b.stride(1),
c.stride(0), c.stride(1),
BLOCK_SIZE_M = 256,
BLOCK_SIZE_N = 256,
BLOCK_SIZE_K = 256,
GROUP_SIZE_M = 8,
ACTIVATION=activation,
num_warps=4,
num_stages=1(close pingpong)
)
return c
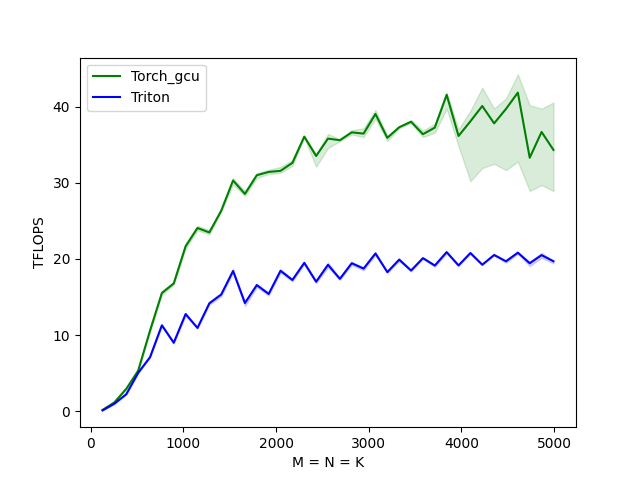
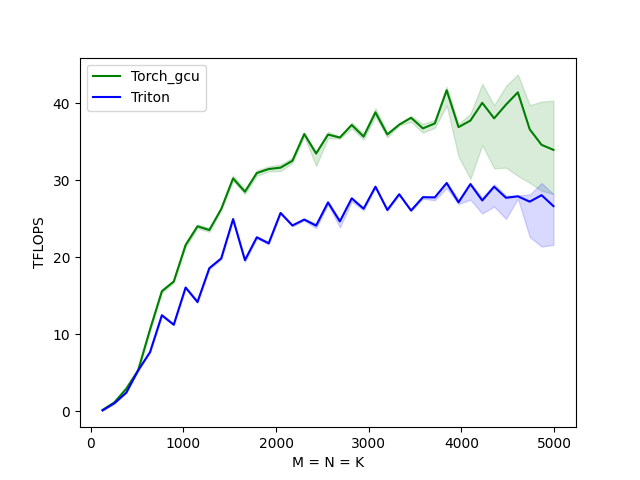
结论:pingpong 开启后,当前场景下有15%左右的性能提升。